Math 185
I took a class that taught us how to use R to analyze things in statistics. This was an advanced elective that presumes general statistics knowledge and is focused on exploring the subtleties between different methods. Samples of the classwork and learnings below.
Power Analysis
Because just knowing the p-value isn’t good enough.
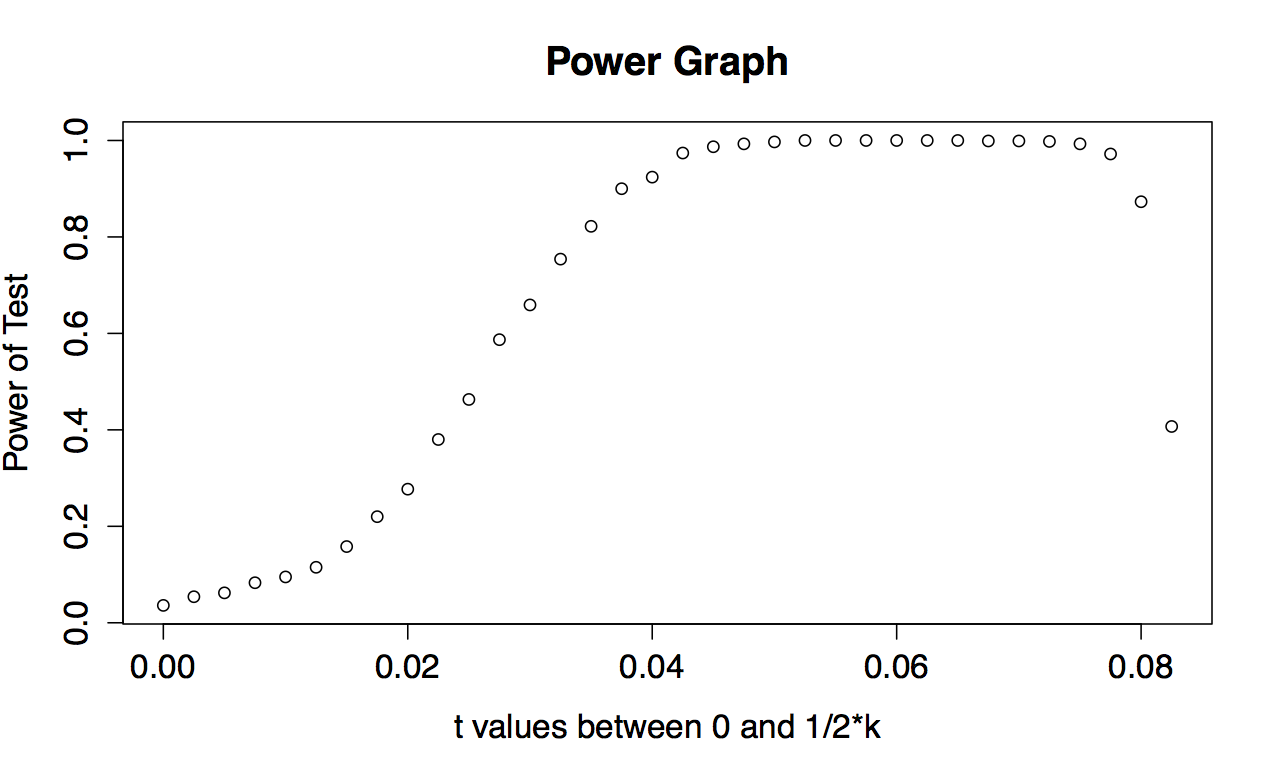
Wrote code that showed how the proportion of samples rejected increases as the the distribution is decreasing in uniformity. T is the value of the difference from uniformity. The power of test is bewteen 1 and 0 and indicates the likelihood of finding an effect that exists given the effect size and sample size.
chisq.power <- function(k, t, n, B = 2000) {
D <- numeric(B) # create a dummy vector to insert output into (initial vector)
P_t <- seq.int(1,2*k) # uniform distribution between 1 and 2k
Pvector <- numeric(2*k)
p1 = 1/(2*k) + t
p2 = 1/(2*k) - t
for (i in 1:k) { # assign probabilities to Pvector
Pvector[i] <- p1
}
for (i in (k+1):(2*k)) {
Pvector[i] <- p2
}
for (i in 1:B) {
x <- sample(P_t, size = 100, replace = TRUE, prob = Pvector)
x = as.factor(x) # convert samples into factors
xtable = table(x) # get counts of factors
if (chisq.test(xtable)$p.value < 0.05) {
D[i] = 1 # set i index of D to 1 if true
}
} # the proportion of samples rejected goes up as t goes up
# as expected since as t goes up, the distribution is decreasingly uniform
mean(D)
}
xvals = seq.int(0, 1/12, 0.0025) # vector of x tick marks
yvals = lapply(xvals, chisq.power, k= 6, n = 100, B = 2000) # get yvalues
plot (xvals, yvals, main = "Power Graph", xlab = "t values between 0 and 1/2*k", ylab = "Power of Test")